Category:

• CAE

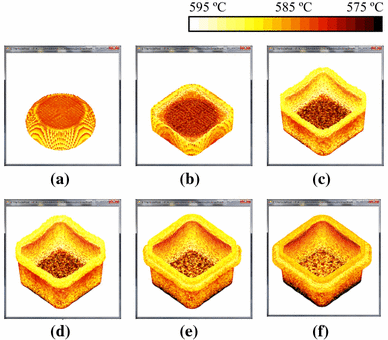
Introduction

The numerical method used in this study is the full implicit moving particle simulation (MPS) method, solves the Navier-Stokes equations in a Lagrangian mesh free framework. The fluid domain is represented by particles, and the motion of each particle is calculated based on the interactions with the neighboring particles by means of a kernel function. The viscosity and pressure calculation of Navier Stokes equation are solved by implicit method. Besides that, the calculation of Kernel function and satisfaction of incompressible condition are done similarly as MPS method, which was originally proposed by Koshizuka and Oka (1996) for incompressible flow simulation. In particular, this implicit particle method used in high viscous flow simulation makes the calculation stable at high kinematic viscosity (1~10 m²/sec) and can solve in large time steps (0.0001~0.00001 sec). The MPS method is similar to SPH (Smooth particle hydrodynamics) method developed by Gingold and Monaghan (1977). In last decade particle based method like MPS/SPH method has been applied in wide range of Nuclear Engineering, Ocean Engineering, Automotive and Chemical engineering etc.

Governing equation

The governing equations for incompressible viscous flows are the continuity and Navier–Stokes equations as follows:

                                                                                                             (1)

                                                                                              (2)

The symbol  is the density, t the time,  the velocity vector, P the pressure, and  the kinematic viscosity.

Particle interaction models

Kernel function

The governing equations written with partial differential equation are transformed to the equation of particle interaction. During interaction the discretized particle domain is smoothed by the smoothing function called Kernel function. In this study, the following function is employed:

                                                                                                              (3)

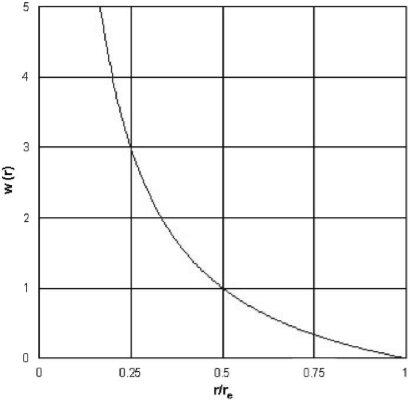
Fig.1. Kernel Function

Gradient model

A gradient vector between two particles i and j possessing scalar quantities f_i and f_j at coordines r_i and r_j is represented as (f_i – f_j) (r_i-r_j)/( r_i-r_j)^2­ as shown in Fig. 2. The gradient vector of each particle i is given by the weighted average of these gradient vectors:

                                                                              (4)

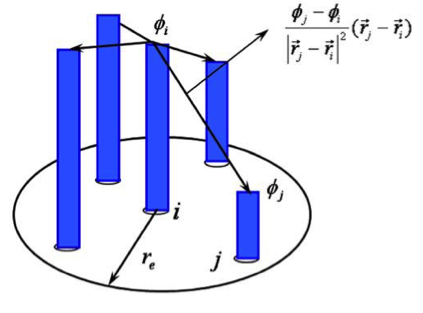Fig.2 Gradient Model

                                                                                                                     (5)

Diffusion model

The diffusiono at particle i is described as

              (6)

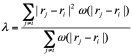                              (7)

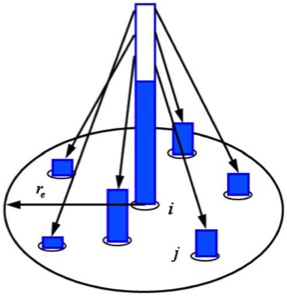
Fig.3. Diffusion Model

Where, Lambda(?) is the parameter by which the varience increase is equal to that of the analytical solution. The diffusion can be modeled by distribution of a physical value from a particle to its neighboring particles by use of the kernel function. As shown in Fig. 3, the model is conservative since the quantity lost by particle i is obtained by the neighboring particle j.

Incompressibility model

Incompressibility is represented by keeping the particle number density constant. After calculation of viscosity and gravity it is assumed that the particle number density n* deviates from n⁰. The particle number density is to be modified to n⁰ by n`:

                                                                                                                                                                                                                                                                                                                                                                                            (8)

Thus, the continuity equation (1) is fulfilled with fixing the particle number density through the simulation. And the modification of the particle number density is related to the modification of velicity v`.

                                                                                                                (9)

Boundary condition

In present study, the kinematic and dynamic boundary conditions are imposed in free surface particles. Free surface particles are judged by particle number density by satisfying condition n*< βn^o. Where β is chossen as 0.98 in this study. The kinematic condition can be directly satisfied by moving particles on the free-surface and dynamic condition is satisfied by making atmospheric Pressure (Patm = zero) at free surface particles.

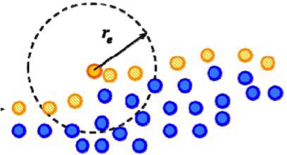
Fig.4 Free surface particles

Algorithm for Full Implicit MPS

The algorithm of incompressibility for the MPS method is similar to that of the SMAC method in a grid system. In which viscosity, external forces and convetion terms are explicitly calculated. But while solving viscosity by explicit process seems unstable and we have to choose extremely small time step which makes calculation, time consuming and extremely unstable to calculate. So, in this paper we had choose to compute viscosity by Implicit method.

In each time there are two stages: in the first stage, the temporal velocity components and coordinates of particle i are obtained using diffusion, external forces, and convection terms, which are implicitly calculated with the values in the nth timestep.

Thus, the temporal coordinates r­_i of particle i can be written using the temporal velocity u_i as follows:

                                                                                                                       (10)

                                                                                                                  (11)

The left hand side of Eq(11) is discretized by diffusion model Eq(6). Since, Velocity is a vector quantity, it has 3 direction (x,y,z). So we need to calculate implicitly in every direction. For simplicity, expanding above equation in x direction only we found:

                                                                                        (12)

Implicit derivation of above equation becomes

                                                                                     (13)

Rearranging above equation

                                                                                      (14)

Matrix formulation of A x = b is represented below

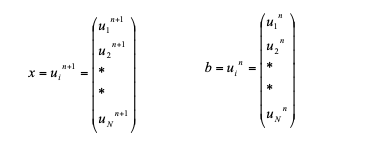
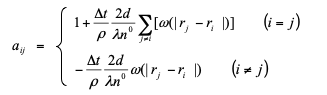
This formation of system of linear equation is solved by matrix iterative method called Conjugate Gradient Method. Thus, conjugate gradient method is solved for 3 times for three direction of velocity vector.

Due to the movement of particles in above implicit mehod, the particle number densities might be changed i.e. n* deviates from n^o. Fig. 5 shows the algorithm procedure of the present method.

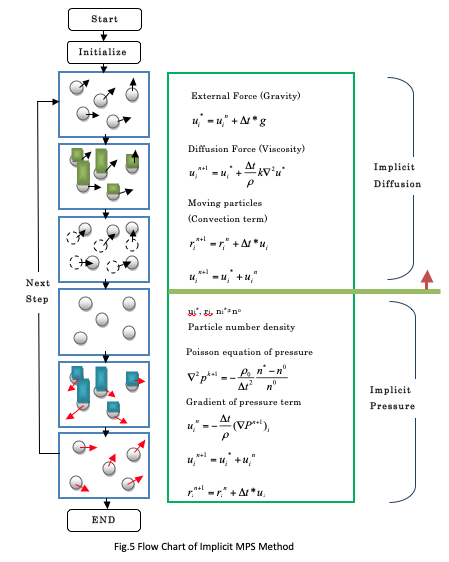
 In second stage, the temporal particle number densities are calculated from the temporal coordinates. The poisson equation for pressure is again calculated implicitly by conjugate gradient method (Koshizuka and Oka, 1996).

                                                                                                                             (16)

                                                                                                  (17)

Rearranging above two equation

                                                                                            (18)

Matrix formulation of Ax = B is represented below

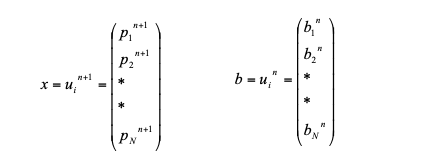
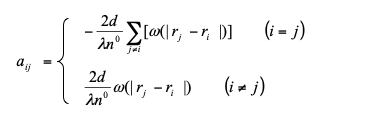
The right-handside of Eq.(18) is represented by the deviation of the temporal particle number density from the constant. Which maintains the particle number densities constant during the simulation. The left-handside of Eq. (18) is discretized by the diffusion model(Eq.(6)). Thus, we have simultaneous equations expressed by a linear symmetric matrix and they are solved by the Congjugate Gradient iteration method.

After calculating the pressure field the velocity is updated by the gradient of pressure which is governed by following Eq. (20).

                                                                                                                             (20)